Benford’s Law is a theory of leading digits in numerical data sets.
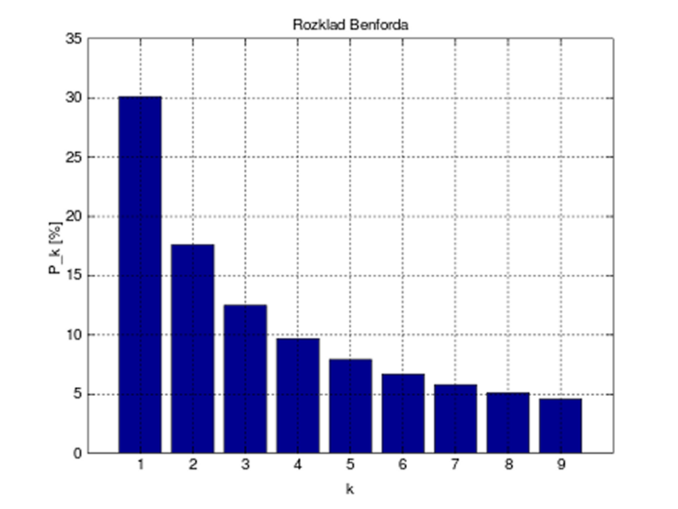
Whilst one might think that the frequency of the leading digit would be equally distributed across the nine digits each with approximately 11% probability, in fact the digit 1 occurs with 30.1% probability reducing to 4.6% probability for the digit 9. Zero is excluded as a leading digit because we might be dealing with numbers such as 0.0189.
Gknor, Public domain, via Wikimedia Commons
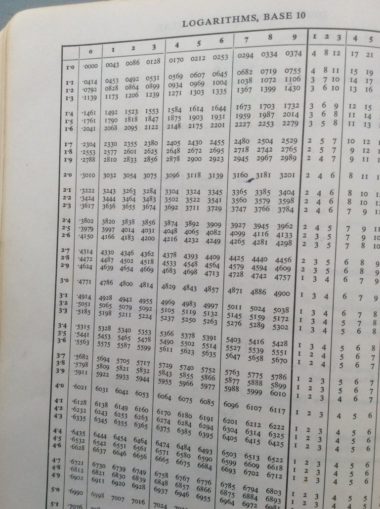
The law was first discovered by Simon Newcomb in 1881 when he noticed that in a book of logarithm tables some pages were much more well thumbed than others.
He propose a law :
\(P(n) = log_b(n + 1) \, – \,log_b(n)\),
where n is the leading digit of a number and b is any base more than or equal to 2.
Read : the probability of n is equal to the log in base b of n +1 minus the log in base b of n.
This can also be written as :
\(P(n) = log_b(1 + 1/n)\)
Using base 10, the log of 1 is zero and the log of 2 is 0.3010.
Thus,
\(P(1) = log_{10}(1 + 1/1) = log_{10}(2) = 0.3010\)
\(P(2) = log_{10}(1 + 1/2) = log_{10}(1.5) = 0.1761\)
It is a slightly easier calculation than :
\(P(2) = log_{10}(3)-log_{10}(2) = 0.4771-0.3010 = 0.1761\)
The results are then used as percentages.
© OldTrout, Going Postal 2020
It was something of a curiosity until it was discovered again by Frank Benford who wrote about it in a paper “The Law of Anomalous Numbers” (1938).
Early proponents of the law suggested that it would be a useful tool in detecting accounting fraud and it is now ubiquitous in forensic accounting including tax evasion.
The law applies to many naturally occurring data sets such as the height of mountains, the surface areas of rivers and populations.
It exhibits scale-invariance (the unit of measurement is irrelevant). It does not matter if mountains are measured in metres rather than feet because that is just multiplication by a constant factor. A set of accounts can be tested in sterling or dollars.
When fraud is being used, the person might think that they are using random numbers, however, patterns usually emerge.
Benford’s Law cannot be applied to data sets which are systematically generated such as telephone numbers. Neither can it be applied to data sets with minima and maxima or not enough order of magnitude such as human heights and weights.
Where Benford’s Law can be applied to data sets there are constraints involved.
The data set should be numeric.
The data set should consist of randomly generated numbers with no minima or maxima and where no numbers are assigned.
The data set should be large. There are different opinions as to what constitutes large, 100 or 1000? The larger the data set, the better the correlation.
Orders of magnitude. This means that the numbers should range through 10s, 100s, 1,000s, 10,000s, 100,000s etc.
Benford’s Law is certainly admissible as evidence in state and federal courts for accounting or tax fraud.
I do not know exactly how it would be used for electoral fraud. I looked at the Pennsylvania results from 2016 before a video was floated by a N.J. forensic accountant using 2020 numbers. The state has 67 counties – is that large enough? There was certainly a range of magnitudes from single digits for some independents through 100s to 100,000s for the main contenders. President Trump’s curve showed some correlation to the law although over represented at the digit 1. Clinton’s showed less correlation as it was underrepresented for the digit 1 and spiked a bit at the 4 digit.
© OldTrout \(2020\)