
An August Conundrum
On August 18th 2024, Mr Stephen Chamberlain was “fatally struck” by a car whilst he was out on an early morning jog in Cambridgeshire. Chamberlain was put on life support after being taken to hospital, [more…]

On August 18th 2024, Mr Stephen Chamberlain was “fatally struck” by a car whilst he was out on an early morning jog in Cambridgeshire. Chamberlain was put on life support after being taken to hospital, [more…]

photo: featured_image.jpg Introduction Note: This article uses Mathjax script. Some script blocking web-browser plugins can prevent the mathematics from been rendered correctly. DM In the first part we looked at how to make a simple [more…]

Introduction “Time is a wayward traveller, who sometimes rides posthaste through thick and thin…” From On The Making Of Gardens by Sir George Sitwell For some strange reason that opening sentence, by Sir George, has [more…]
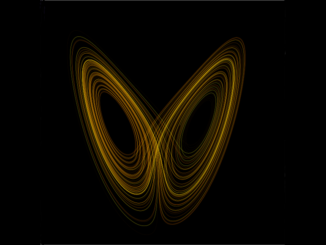
On Dec 29th 1972 a paper was submitted to the American Association for the advancement of Science. The author, Edward Lorenz was an MIT professor of meteorology and the subject of the paper was:- Predictability; [more…]

Have you ever wondered how the bank worked out how much interest to pay on your savings account, or charge you on your mortgage? I had a mortgage with a building society some years ago, [more…]

Science, like a sport, is an art that’s well practised. To lose educates you more than to win instantly. Okay, that’s corny but I’ve found that my project failures have taught me more information and [more…]

Think for a moment about a field, half filled with rabbits. How can we figure out how many fluffy bunnies we’ll have in a year’s time? Let’s start by agreeing to use a population of [more…]

Question: Do snails understand mathematics? Ok here’s an idea. Start with the value 0 and 1 and then apply the following rule. Take the last 2 numbers you have and then add them, to make [more…]

Fracking is once again in the news, once again you will hear of the dire consequences, the disasters and the earthquakes caused by drilling and fracturing the shale underground. It was suggested that the proposed [more…]
Copyright © 2025 | MH Magazine WordPress Theme by MH Themes