As promised in part two we will now construct an experiment to demonstrate acceleration under gravity, show how vectors can be “resolved” into a 2 dimensional plane (3 three dimensional if you fancy the extra work) and also how the third law works.
Recap, Three laws of motion
First Law
In an inertial frame of reference, an object either remains at rest or continues to move at a constant velocity. Unless acted upon by a force.
Second Law
In an inertial frame of reference, the vector sum of the forces \mathbf{F} on an object is equal to the mass m of that object multiplied by the acceleration \mathbf{a} of the object: \mathbf{F}=m\mathbf{a} (it is assumed here the mass is constant)
Third Law
When a body exerts a force on a second body, the second body simultaneously exerts a force equal in magnitude and opposite in direction on the first body.
Moving Onwards, and Downwards
In part two we demonstrated the first and second laws, and showed how to prove the first, now we will demonstrate a physical proof of the second and third.
What we want to do is measure the acceleration from gravity on an object, we will do this in two ways, the first will be hypothetical and determine what we expect to happen, we can then look at this in a physical experiment and see what results we get.
Now we can, as outlined in the last part simply drop something and time it, the trouble is timing it accurately, if you have the equipment to do this however then it works nicely – photo cells or beams that can measure when cut etc.
For the rest of us though limited to what we can re-purpose from around the house we need something easier.
This version of the experiment looks thus:
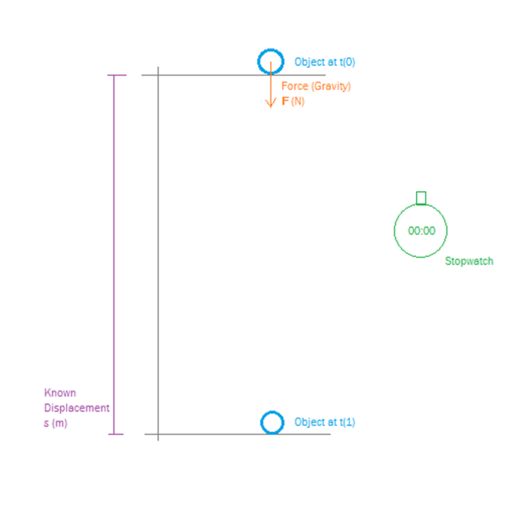
The experiment works thus, the object is held at a known vertical displacement above a surface and is held still. Then at t_0 the object is release and the stopwatch started, and stopped at t_1 when the object first touches the surface below it.
From this we know the time duration (t), initial velocity (\mathbf{u}=0), the displacement (\mathbf{s}=1), the objects mass (m=1). what we wish to determine is acceleration of the object due to the force of gravity (\mathbf{a}), and the force of gravity (\mathbf{F}).
Examining our list of equations we find \mathbf{s}=\mathbf{u}t+\frac{1}{2}\mathbf{a}t^2, this contains only things we know with a single unknown (\mathbf{a}), so by a bit of numeric jiggery-pokery we can re-arrange this to determine (\mathbf{a}).
1. \mathbf{s}=\mathbf{u}t+\frac{1}{2}\mathbf{a}t^22. 2(\mathbf{s}-\mathbf{u}t) = \mathbf{a}t^2
3. \mathbf{a}=\frac{2(\mathbf{s}-\mathbf{u}t)}{t^2}
Proper numbered equations, its almost as it I know what I’m doing… almost…
now this is the formula to use for the experimental version where you measure (t), for the theoretical version we know the acceleration from gravity and will calculate the time – then if the time calculated matches the time measured our assumption for the acceleration is correct.
We calculate the time to be 0.45 seconds, as you can see this is a bit tight to actually measure with typical reflexes etc.
Ok, so experimentally we need a way to slow the acceleration down, if you can find a way to significantly change the force of gravity you will end up very rich, so we need a way to simulate this. We can do this by rolling our marble down a slope and not just dropping it.
Our object is 1kg, we are going to assume zero friction so we don’t have to worry about rotational inertia here – in the real world a marble is of low enough mass it won’t really matter.
We now need to consider a bit of the third law and look at how things on slopes work, consider the following.
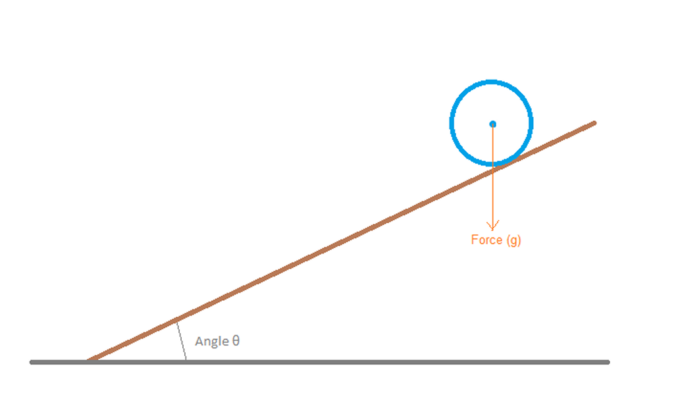
“common sense” says the object will move down the slope, but why? And how can this be calculated?
We need to consider the forces acting upon both our object, and the slop itself, these force can only act where the two objects meet and are this:

The forces acting on the object are the Force Gravity (\mathbf{g}) and Force Reaction (\mathbf{F_r}), the force acting on the slope is Force Action (\mathbf{F_a}).
We now need to consider the effect of these forces, since we are only really bothered about the object we will consider this first. We need to resolve this force into elements, the first parallel to the slope, the second perpendicular to the slope. This is handed by basic trigonometry thus:
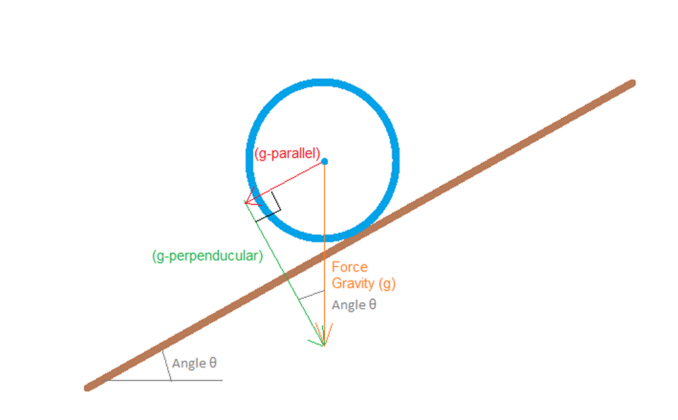
We can resolve these forces using Pythagoras thus:
4. g_{parallel} = \mathbf{g}.sin(\theta)5. g_{perpendicular} = \mathbf{g}.cos(\theta)
does this match what would be expected? Well set the angle \theta=0 and the parallel force becomes 0 and the perpendicular force becomes equal to \mathbf{g}, the angle to 90 degrees and the parallel force becomes equal to \mathbf{g} (straight down) and the perpendicular force (horizontal) becomes 0.
By doing this we can, in effect, vary the effect of the force of gravity on our object for the purposes of accelerating it down the slope, it will be accelerated by the parallel force only. This also matches expectations, things roll faster down steeper slopes.
So now we can re-set out experiment thus, and gain something more practical to undertake.
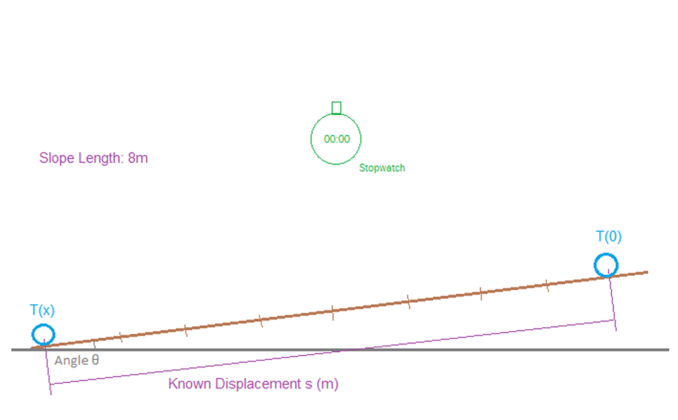
Using what we have seen before we now set up a slope of a known displacement, here shown as 8m, doesn’t matter though as long as the distance is known, we will set the angle to 20 degrees.
Again for the calculation we are using the known value of gravity, and will then match the time experimentally to confirm.
The force acting to accelerate our 1kg object is thus:
6. \mathbf{F}=9.81.sin(20)7. \mathbf{F}=3.356N
Note that in practice you can also simply resolve the acceleration, the mass of the object is essentially irrelevant as long as in the practical version it is large enough to over come rolling friction while not being large enough to care about rotational inertia.
Calculation shows with this acceleration we should take approximately 2.18 seconds to roll the 8m, if we again split this time into equal length periods we can witness the acceleration in action
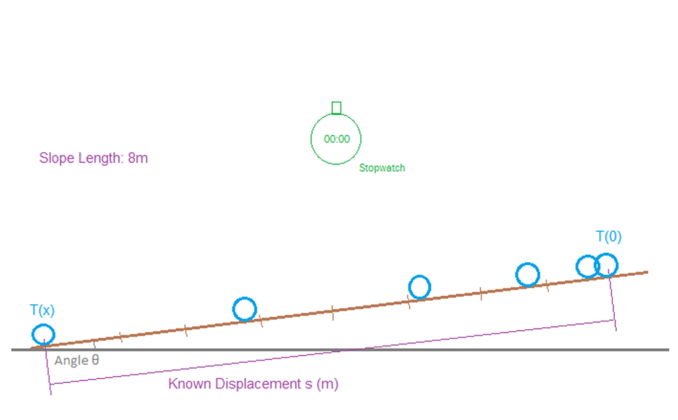
If this is set up with different angles and different lengths the results will of course vary in terms of time, but working backwards you will have a pretty good approximation for the local force of gravity.
Just one more thing…
we have until now only considered the effect on the object and assumed the slope is fixed, but what if it wasn’t? what if the slope itself was on a frictionless surface?
We have resolved the forces acting upon the object, for Newton’s third law to be true they must equally act with opposite direction upon the slope, now the slope can only move horizontally, so we have a force of 3.356 N acting up the direction of its slope, we can again resolve this force into a horizontal element (which will cause an equal reaction from the ground, in addition to the reaction caused by the mass of the slope being acted upon by gravity) and a horizontal force.
This is again calculated by trigonometry and is calculated thus:
8. \mathbf{F} = 3.356.cos(\theta)
If the surface is horizontal then 100% of the objects parallel force is transferred to it (though in that case the force being transferred is zero) and if the surface is vertical then none of the objects parallel force is transferred to it.
Here the force resolves as: 3.15 N, if we assume the slope has a mass of 50 kg the slope itself will accelerate at (via \mathbf{F}=m\mathbf{a}): 0.063 ms^-2>. With a frictionless surface below it, as the object moves down the slop to the left, the slope itself will move 0.14m to the right, both objects will then continue with their final velocities until some other force stops them.
Because of the difficulties of actually doing this it’s a bit harder to test this, but it can be done using slightly heavier masses to overcome friction.
It would look roughly thus:
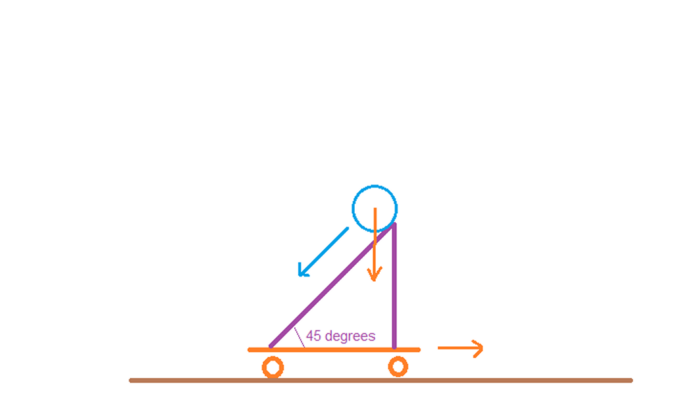
The 45 degree angle provides the maximum horizontal force on the skateboard the slope is balanced upon, stick something like a bowling ball on it and let go, both the ball and the skateboard will move, if you suitably measured the velocities and times you would be able to work the calculations backwards and validate Newton’s third law experimentally.
This concludes the third part of this series, we have covered the basic laws of motion concerning constant linear acceleration, and demonstrated ways in which can be confirmed experimentally to provide an accurate representation of the physical world, within a few constraints related to ensuring the velocities are low enough air resistance doesn’t matter and the masses high enough they can overcome friction, without being too high so we can ignore rolling inertia.
In the next parts we will start to look at the physics of rotation and constant rotational acceleration and rotational inertia, plus the curious case of “centrifugal force” and “centripetal acceleration”
Featured image: NASA [Public domain]
© Leopard 2020
The Goodnight Vienna Audio file
Audio Player


