Playing With Electricity – Part 4

Damn You Morus Nigra!

‘John Swerved as Mary, Queen of Scots, was busy with her throne but it wouldn’t flush so her face turned to stone when Jane put her hand on John’s gear stick which began to vibrate and she became wet as it started to rain she pressed her bosom into his chest as she trimmed his mullet which then flew off when he stud suddenly erect in her summer house…’

“Peabody! Leave the club typewriter alone will you!?”
“*errgh!* Just trying to help and at least my writing is entertaining and makes sense…unlike your wubbish…”

…and Peabody makes a good point. The one thing (among many things) that I love about mathematics is that it completely screws with your brain. What logically should be right invariably turns out wrong and vise versa. I call the process ‘dancing around the mulberry bush’. While I think that I’m learning how to brush my teeth on a cold and frosty morning I’m actually just staring at a pile of soiled underpants!

And so it is with trying to explain voltage and current. This article is supposed to present some of the mathematical principals involved and is supported by a simple experiment but it’s really just a bit of fun – buyer beware/caveat thingy and all that. Overall, I hope it provides some food for thought and a little entertainment along the way.

Voltage, Current, Resistance, Power, Time And Uncle Tom Cobley

Put simply, current is how much voltage can flow around a circuit in a unit amount of time. The power is the product of said voltage and current which is usually measured in watts (lower case like newtons because common noun stuff). The flow of current is restricted by circuit resistance (measured in ohms) and the time unit is measured in seconds and mass will be measured in kilograms and energy in joules or watt seconds and God is in his heaven…let there be light…jolly good. As clear as a Fanny Craddock tagliatelle recipe. Glad I could help.

The header photo shows Mr Three-pin in his car all revved-up but he has no road on which to travel. You might recall my silly joke about electrical circuits and Formula One race tracks in part 1 – no? I don’t blame you it was rubbish but it is a good analogy. Let’s think of Mr Three-pin’s car, perhaps a Volts-wagon (come on, it took me ages to think of that!), travelling around such a circuit. On the circuit there are some obstacles (resistances) which will slow him down.

Suppose there are five Volts-wagon cars in the race and that all five cars complete the circuit in 1 minute. Mathematically that’s: ${{5 \text{ cars}} \over {1 \text{ minute}}}={5 \text{ cars per minute}}$ .

Now suppose that we increase the number of obstacles on the circuit and only three cars cross the finish line in 1 minute. To get more cars completing the circuit in 1 minute we need to do at least one of two things as the speed of the cars is fixed like an electron: 1) reduce the number of obstacles (reduce the resistance) or 2) increase the number of Volts-wagons taking part thus increasing the likely hood that five cars will pass the finish line in 1 minute. This is exactly how all electrical circuits work. The road circuit – instead of being made of tarmac and the like – is made from copper wires and electronic components that all offer up an electrical resistance to the flow of electrons (our Volts-wagons).

The number of Volts-wagons that complete the circuit in 1 minute is called the intensity (I) which is what we now call the amp. (A) for measuring current. Named after André-Marie Ampère whose work he called Intensité du courant which is where we get the letter ‘I’ from. Now get ready to join the mulberry bush dance or perhaps to be smacked around the head by it. Well here goes:

$\text{1) }I = {dQ \over dt}$

$Q$ is the electrical charge and is measured in coulombs $C$ and we can therefore write $Q = C$ , think of $Q$ as standing for quantity. So far so good but we need to ‘convert’ $C$ into $V$ or volts. To do that we need to introduce Mr James Watt’s law which is mathematically stated by this equation:

$\text{2) }W = I \cdot V \text{, and importantly } V = {\mathit{W/s} \over \mathit{I/s}}$

Where (W) watts is equal to (I) amps times (V) volts the $‘/s’$ means ‘per second’ which, unfortunately, needs to be explained as best I can!

Firstly, $W/s$ is pronounced ‘watts per second’ and $W \cdot s$ is ‘watt second(s)’ and the same goes for any other value e.g $m/s$ is meters per second etc. Both have different meanings: one is division the other multiplication. In mathematics we can think of ‘quantities of something’ in two ways:

1) Not changing or constant for all time. E.g: 100 apple pies. They’ll just sit there forever if left alone and there’ll always be 100 apple pies, no more, no less. Mathematically we could write $A_{pies} = 100$ .

2) Changing or ‘in flux’ as good old Sir Issac Newton would say. E.g: 100 apple pies per minute. Imagine a food factory’s conveyor belt constantly turning out 100 apple pies every minute 24/7. After 1 day we’d have 144,000 pies, after one year we’d have nearly 53 million apple pies. Mathematically we could write: $A_{pies} = 100/ \text{minute}$ .

The same goes for our electrical quantities. We can have 1W constantly or 1W cumulatively ‘summing (or adding) up’ per unit of time. We are all familiar with our electric bill, Ed you…rather not say. It’s calculated from the total amount of kilo-watts used per hour or $kW \cdot h$ or $kWh$ for short.

If you boil a $2400W = 2.4kW$ kettle for 3 hours (what the hell sort of kettle that is I don’t know!) you would have used a total of $\mathit{7.2kWh}$ or $\mathit{2.4kW/h+ 2.4kW/h + 2.4kW/h = 7.2kWh}$ . Mathematically we say that $\mathit{kW/h}$ is the derivative of $kWh$ and $kWh$ is the integral or sum of $\mathit{kW/h}$ , written:

$\mathit{kW/h} = {\mathit{dkWh} \over dt} \text{, and } \mathit{kWh} = \int \mathit{kW/h} \; dt \text{, where t is time in hours}$

What we can take from all this is that the faster you do something the more energy you have to put in and consequently the more energy you’ll get out of a system. E.g: A $2.4kW$ kettle might boil 1 litre of water in 3 minutes but a $7.2kW$ kettle would do it in 1 minute.

The definition of $1C$ is one volt flowing through a resistance of one ohm for one second which is equal to one amp per second. We can see from the above equation (2) that a $2400 Ws$ kettle drawing $10 Is$ (or ten amp seconds) equates: $2400Ws \div 10Is = 240V$ . So, $C = \text{ amp seconds }$ therefore $Ws = C \cdot V$ or coulomb volts and $1Ws = \text{ 1 Joule}$ . How ya’all enjoying that mulberry bush – anyone else fell over yet cuz I know I have!?

Our road analogy has obstacles in the car’s way which slows the traffic down. The mathematical law that quantifies how much the electrons are ‘slowed down’ is called ohm’s law named after its creator Georg Ohm and is measured in, you’ve guessed it, ohms which is represented by either the Greek letter $\Omega$ or just $R$ for resistance:

$R = {V \over I} \text{, therefore } I = {V \over R}$

The resistance of a circuit or device is often referred to as the ‘load’. Now if you compare that last equation, $I=V/R$ , to our first equation (1) you can see that they are very similar. We’ve established that resistance $(R)$ ‘slows down’ $(t)$ or restricts the movement of electrons the larger its value. So the current $I$ becomes larger the smaller the value of $R$ or $t$ therefore the watts needed/generated becomes greater the quicker you move the electrons around. Now, I know what you’re all thinking at this point: Einstein’s special relativity and mass/energy conservation. The Doc can’t pull the wool over the GP crowd’s eyes! So let’s shaft the genius’s famous equation like this (he won’t mind, he hated mathematics anyway):

$E_{joules}=m_{kg} \cdot c_\text{speed of light}^2 \to E = V \cdot Q \cdot t^{-1}$

All I’ve done is exchanged mass for charge in $Ws$ and multiplied it by the reciprocal of time in seconds to change it to frequency $(1/t \text{ replaces } c)$ . Well, I mean, the effect is much the same as a big red button. Let’s have a play with old Einstein’s tosh. Let’s see how many mugs of tea we could make with just one kilogram of coal turned into pure energy:

$J = 1_{kg} \cdot 3E8_{m/s}^2 = \text{ 9E16J or 90,000,000,000,000,000J}$

Yeah, that’s a mere 90 petta watt seconds as 1J is equal to 1Ws. Let’s assume that it takes a 3kW kettle 60 seconds to boil a mug of water. So, $90PWs \div (3000Ws \cdot 60s) = 5E11$ or $500 \text{ billion}$ mugs of tea. You’ll need a bigger China and a heck of a lot of biscuits!

A Spot Of Welding

That shows that doing things really fast in physics makes stuff go with a big bang! We can do a simple experiment with our little equation to demonstrate this point. Here’s a simple spot welder:

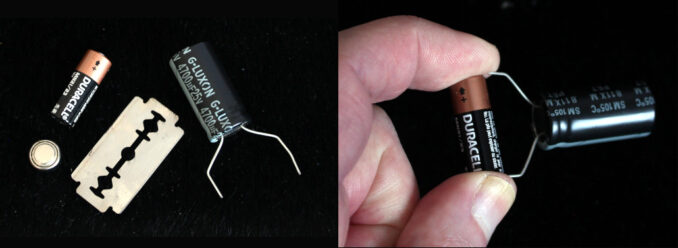
As you can see it’s made from just three components: a 12 volt 23A ‘key fob’ battery (LR44 1.5V battery for scale as the 23A is just eight similar ‘button’ batteries stacked in series), a 4700uF capacitor and a razor blade (actually that’s what we’re going to weld). A 23A battery is rated at about 55mAh or 55 milliamp (1000th of an amp) hours and an electric welder is rated at anywhere from 40Ah to 400Ah or a minimum of 1000 times what our little battery can deliver. What we need to do, as the mathematics above shows us, is to ‘speed-up’ the flow of electrons from the 23A battery and that’s where the capacitor comes in.

A capacitor is close to an ideal battery but nowhere near perfect: fast to charge and fast to discharge. You might have read the warning label stamped on most batteries: Do Not Short Circuit! And very good advice it is too as doing so will mess up your day quicker than the Labour party can steal your money. The thing is that’s what we want to do (short circuit, not steal money) as that’s exactly how an electric welder works. Batteries are lazy, they don’t like giving up their electrons. Not so a capacitor – it’ll hand them over quicker than the Labour par…oh, I’ve done that one.

In the photo, above, you can see me charging-up that capacitor to 12V. This only takes a second or so. Now let’s see what happens when we short circuit the thing on some thick kitchen foil:

*Demonstrating what happens when you make $t$ small*

Quite impressive from such a small battery – I’m shorting the capacitor from underneath the foil and you can see that it has ‘blown’ holes clean through. Nice.

Let’s maff that to see what happened. Okay, a capacitor’s electron storage capacity is measured in farads and $1F$ is equal to 1 million micro farads or $0.000 001F$ . Our capacitor is rated as $4700 \mu F$ (4700 micro farads) or $0.0047F$ . Good. Now it turns out that $1F$ can store 1 Coulomb per volt so our capacitor stores $0.0047F \cdot 12V = 0.0564C, \text{and } Q = C$ or $56.4mAs$ . That’s not much but let’s introduce our good friend Mr Time with our modified mass/energy equation. Let’s say that our capacitor can deliver that tiny amount of energy not in 1 second but, say, 10mS or 100 times faster – then we get:

$I_{amps} = Q_{charge} \cdot t_{seconds}^{-1} = 0.0564 \cdot 0.01^{-1} = 5.64Amps$

That’s $5.64A \cdot 12V = 67.68W$ or nearly 68 watts in 10mS! Let’s see if that’ll weld a razor blade to the capacitor’s leads:

That’s why switch contacts have to be made from a hard metal. Just for a final bit of maffs fun let’s compare the amount of energy from our little welder to the pure energy released from the lump of coal.

We know that $Ws_{(Joules)} = C \cdot V$ so our capacitor is holding $0.6768Ws$ . The 1 kg lump of coal turns into $90E16J \text{ or } 90PWs$ :

$90PWs \div 0.6768Ws = 1.33E17 \text{ or } 133,000,000,000,000,000$

…therefore our capacitor holds/releases…

$(1.33E17^{-1}) \cdot 100 = 7.5E-16 \text{ or } 0.000,000,000,000,000,75 \text{%}$

Which equals 0.75 femto-percent (I think!) of all the energy in the lump of coal. Still, it was just enough to spot weld the razor blade.

Well, I was going to talk more about that little motor but I seem to have run out of space and time, so here is a nice photo of me and Peabody taken c.1884 with our Semmendinger wet plate camera and Voigtlander lens: