In The Basel Problem we saw that Euler answered the question by showing that the sum of the reciprocals of the square numbers is equal to \(\pi^2/6\).
That is
\(\displaystyle \sum_{n=1}^\infty \frac {1}{n^2} = 1 + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \frac{1}{5^2} + … = \frac{\pi^2}{6} \)
The partial sums slowly converge to the limit of \(1.644 934 066 …\).
It was a remarkable proof that utilised the Taylor/Maclaurin series of the sine function, hence the appearance of \(\pi\).
\(\displaystyle \sin(x) \approx x-\frac{x^3}{3!} + \frac{x^5}{5!}-\frac{x^7}{7!} + …\)
IkamusumeFan [CC BY-SA]
Two years later, in \(1737\), Euler published a paper proving that this infinite sum over all the natural numbers, \(\Bbb N\), is equal to an infinite product over all the prime numbers, \(\Bbb P\).
This is the first key to the riddle of the primes.
Once again Euler shows his dexterity, this time by using the sieve of Eratosthenes.
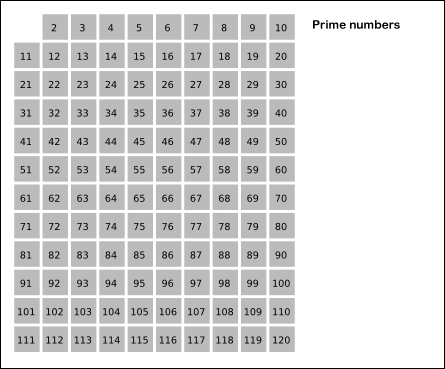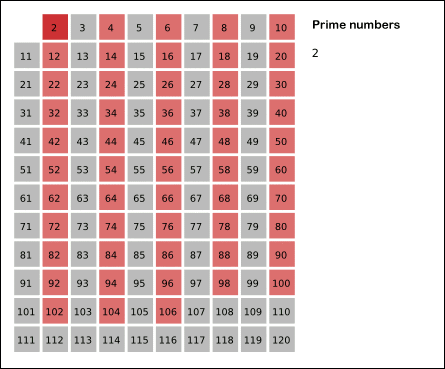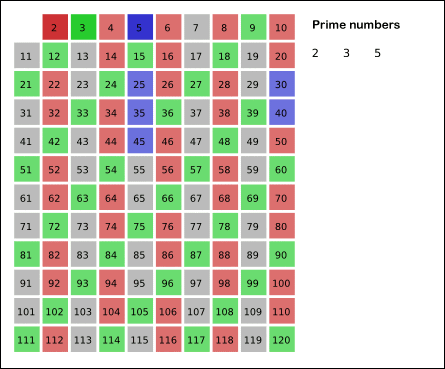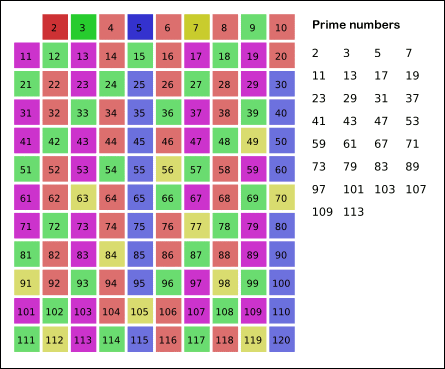
SKopp at German Wikipedia [CC BY-SA]
\(\displaystyle \frac{\pi^2}{6} = 1 + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \frac{1}{5^2} + \frac{1}{6^2} + \frac{1}{7^2} + …\)
Multiply both sides by \(1/2^2\) :
\(\displaystyle \frac{\pi^2}{6}\cdot\frac{1}{2^2} = \frac{1}{2^2} + \frac{1}{4^2} + \frac{1}{6^2} + \frac{1}{8^2} + \frac{1}{10^2} + \frac{1}{12^2} + \frac{1}{14^2} + …\)
Subtract the second equation from the first equation:
LHS :
\(\displaystyle \frac{\pi^2}{6}-\frac{\pi^2}{6}\cdot\frac{1}{2^2} = \frac{\pi^2}{6}\left(1-\frac{1}{2^2}\right)\)
RHS :
\(\displaystyle \left(1 + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \frac{1}{5^2} + …\right)-\left(\frac{1}{2^2} + \frac{1}{4^2} + \frac{1}{6^2} + \frac{1}{8^2} + \frac{1}{10^2} + … \right) \)
\(\displaystyle = 1 + \frac{1}{3^2} + \frac{1}{5^2} + \frac{1}{7^2} + \frac{1}{9^2} + \frac{1}{11^2} + \frac{1}{13^2} + …\)
Thus :
\(\displaystyle \frac{\pi^2}{6}\left(1-\frac{1}{2^2}\right) = 1 + \frac{1}{3^2} + \frac{1}{5^2} + \frac{1}{7^2} + \frac{1}{9^2} + \frac{1}{11^2} + \frac{1}{13^2} + …\)
We repeat these two steps for all the prime numbers :
\(\displaystyle \frac{\pi^2}{6}\left(1-\frac{1}{2^2}\right)\left(1-\frac{1}{3^2}\right)\left(1-\frac{1}{5^2}\right)\left(1-\frac{1}{7^2}\right) … = 1 \)
The RHS has been sieved; the primes are on the LHS and the multiples of primes have disappeared.
Solving for \(\pi^2/6\) gives :
\(\displaystyle \frac{\pi^2}{6} = \frac{1}{\left(1-\frac{1}{2^2}\right)\left(1-\frac{1}{3^2}\right)\left(1-\frac{1}{5^2}\right)\left(1-\frac{1}{7^2}\right) …}\)
This is the Euler product (there are others).
We write it as :
\( \bbox[15px,border:2px solid black]
{
\displaystyle
\sum_{n=1}^\infty \frac{1}{n^2} = \frac{\pi^2}{6} = \prod_p \frac{1}{\left(1-\frac{1}{p^2}\right)}
}
\)
© OldTrout \(2020\)



