A Triangle

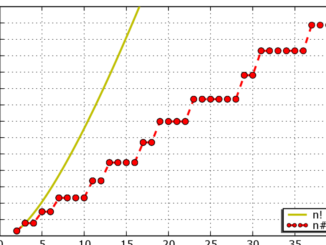
This is Klauber’s Triangle : –

He produced it in the 1930s.  The underlying numbers are the natural numbers ℕ and are arranged as follows : –

In the image the prime numbers are blue and the red-highlighted numbers are solutions to Eulerian polynomials.

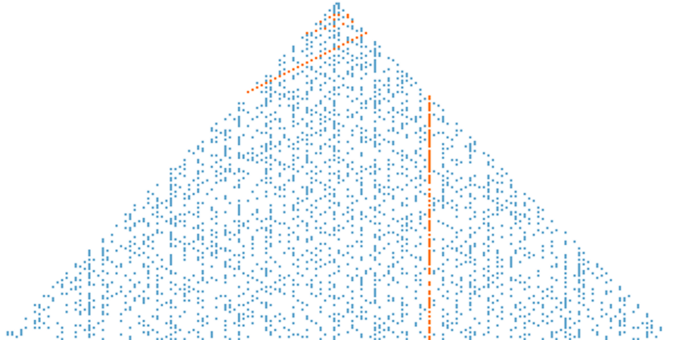
This a triangle which I discovered about five years ago : –

The prime numbers are white and the secondary, composite numbers are black.

The underlying numbers are the odd numbers and are arranged as follows : –

Label each row n = 1, 2, 3, . . .

From the left-hand side, the pairs of numbers add to 2n on even row numbers.  On odd row numbers, the last number is added to itself to equal 2n.

By the Odd Number Theorem, the sum of each row is n².

Again from the left-hand side, the pairs of numbers multiply to n² – a².  On odd numbered rows the last number is multiplied by itself.

For example

• n = 6,  1 x 11 = 11 = 6² – 5²,  3 x 9 = 27 = 6² – 3²,  5 x 7 = 35 = 6² -1².
• n = 7,  1 x 13 = 13 = 7² – 6², 3 x 11 = 33 = 7² – 4², 5 x 9 = 45 = 7² – 2², 7 x 7 = 49 = 7² – 0².

I believe it to be a Turing pattern (a reaction-diffusion system).  It displays many of the signatures; waves, stripes, spots and hexagons.

An interesting feature is that π/2 is also embedded in the triangle.

Note that the numbers in the right-hand diagonal are 1, 3, 3, 5, 5, 7, . . . These are the numbers that occur in the denominator of the Wallis Product.  The numbers for the numerator are found in the number of addends in each row. Thus, row n = 1 has addends 1 and 1 which is 2.  Row n = 2 has addends 1 and 3 which is also 2 and so on.

π       2 • 2 • 4 • 4 • 6 • 6
–  =  ––––––––––––––– . . .
2       1 • 3 • 3 • 5 • 5 • 7
 

© OldTrout 2016