
User:Solipsist (Andrew Dunn) / CC BY-SA
If you pick something up and lift it, this takes effort, if you let go it will fall, but why?
We know objects, such as leopards, have a mass (m) as a fundamental property, we also know that left to their own devices objects, such as leopards, try not to move unless provoked.
Yet if you hold something and let it go, that something generally falls towards the ground, why? Its not as if you have provided a force upon it to make it move is it? So who has?
This is something that has puzzled inquisitive people over the ages, our favourite apple target, Isaac Newton also pondered on this, he came up with a “universal law of gravitation”, which so long as the objects you consider are not truly massive or moving with a truly high velocity pretty much holds true. The bloke with the crazy hair, Einstein, later came along and provided a more accurate “law” but for most purposes the differences are small enough not to worry about.
For example satellite orbits and interplanetary probes are usually put into orbital paths developed using Newton’s work as it’s a lot easier to work with.
The theory basically says “everything attracts everything else in proportion to its own mass and the distance between the objects”, mathematically this works thus:
F = G * ((m1 * m2)/r2)
On its own the formula didn’t work, the addition of G, a constant value, makes it work, this is the “gravitational constant”.
Here r relates to the distance between the centres of mass where the two masses are said to act.
Note that Newton’s third law holds true, if one object exerts a force upon another, the other returns the favour, the same formula is used but you can see the masses are interchangeable, since the displacement between the masses is inverted if the frame of reference is constant (i.e. one is to the left of the other, the other is to the right of the first) this will correctly invert the direction of the force.
This is visualised thus:
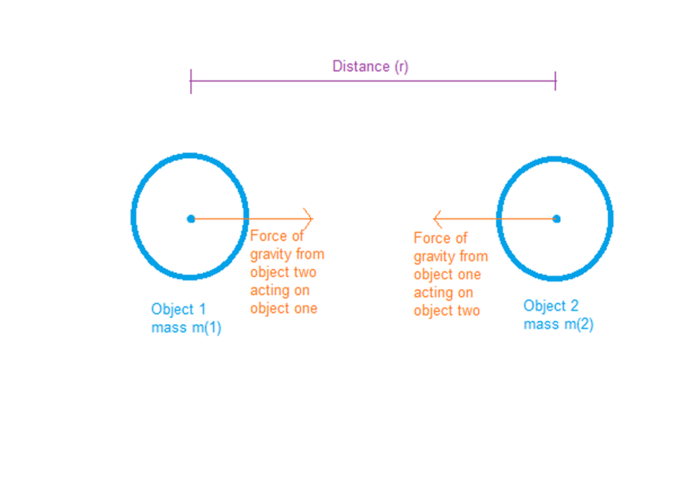
If nothing else applies this is going to result in the objects experiencing an acceleration towards each other.
This is incidentally partly how planets etc are formed, they are hold together by mutual gravitational attraction. Note that as atoms get close other forces take over and stop them getting too close but in broad terms this is why planets stay together, the various bits they are made from attract each other.
This also works when the masses of objects are not in the least bit similar, e.g. you yourself are experiencing a force from the planet Earth’s gravity which pulls you towards its centre of mass, but the planet earth is also experiencing a force from yourself pulling it towards your centre of mass.
As an aside this is why planets try to be round, this is the lowest energy state. We have yet to consider potential energy and kinetic energy, however a sphere has the lowest surface area for a given volume and is the shape “stuff” naturally tries to form. If they were any other shape they would not be at the lowest energy state.
Asteroids and smaller moons are often irregular as while gravity is trying to make them round they lack enough mass to actually collapse into a ball compressing the stuff they are made from.
Now actual verification of gravity is somewhat difficult in the kitchen, you can measure the effect of the earth’s gravity on an object, but measuring the effect of the object upon the earth isn’t happening. Also a typical kitchen isn’t large enough to contain objects that attract each other enough to measure.
It can however be observed indirectly by looking upwards at the moon.
The system looks thus:

We will be returning to the orbital side of all this later, however we can calculate the gravitational forces the earth and moon exert upon each other using the equation from before thus:
F = G * ((m1 * m2)/r2)
F = 1.98×1020N
This is the force both bodies exert upon the other, this causes the earth and the moon to accelerate towards each other…
Now you may have noticed that the moon hasn’t crashed into the earth, and this is because this is not the only thing going on here. Both bodies are orbiting around the other, at a common centre of mass – in effect if you could stick them on a long and strong enough ruler the point at which it would balance.
Hmm. So where is that point?
We can work it out using the rotation principle of moments, because the system is (essentially) in equilibrium the forces in one direction must match the forces in the other, thus:

Consider the purple dot, which will be the centre of rotation as our pivot. We know from the consideration of rotation that with the system in equilibrium (the distance is constant, as is the angular velocity) there is no angular acceleration, thus no torque acting.
Thus the following must be true:
Massearth * Rearth = Massmoon * Rmoon
Now we know both masses but not either radius, but we can work out the ratio between them thus:
Massearth / Massmoon = Rmoon / Rearth
We end up with this
Rmoon / Rearth = 81.34527
So the balance point is 81.34527% along the line from the moon to the earth (the earth being heavier its nearer the earth than the moon)
The point is thus:

Note this point is not only not “the centre of the earth”, its not even within the earth. The place actually has a useful function – anything sitting there has the force of gravity from the earth and the moon equal, so it will just sit there.
This is known as the Lagrange point, after some bloke who probably didn’t have apples thrown at him.
Now for this to be “true” there must be something stopping the earth and moon colliding, that something is due to the rotation and we will consider it in the next part.
© Leopard 2020
The Goodnight Vienna Audio file



