Or : Multiplying by \(i\).
The beginning of complex numbers is often attributed to Cardano (1501 – 1576). Complex numbers provide a solution to the equation \(x^2 = -1\).
They are an extension of the number system from \(\Bbb R\) (the real numbers) to \(\Bbb C\) (the complex numbers).
Complex numbers take the form :
\(z = a + bi\),
where \(a,b\) are real numbers and \( i = \sqrt -1\).
The normal rules of arithmetic and algebra apply with the additional rule that :
\(i^2 = -1\)
When two complex numbers are multiplied together the real numbers, \(a\) and \(b\), act as scalars and the imaginary number, \(i\), acts as a rotation about the origin, \(0\), (counter-clockwise from the positive real axis). Multiplication by \(i\) on its own leads to a rotation of \(\pi/2\) radians in the complex plane.
\(\begin{align}1\cdot i & = i & = i\\
i\cdot i & = i^2 & = -1\\
-1\cdot i & = i^3 & = -i\\
-i\cdot i & = -i^2 & = 1 \end{align}\)

Starting at any point on the real axis, (Re), and repeatedly mutilplying by \(i\) traces larger or smaller circles.
The multiplication of two complex numbers gives another complex number.
Let :
\(z = a + bi\) and \(w = c + di\)
Then :
\(\begin{align} zw & = (a + bi)(c + di)\\
& = ac + bdi^2 + adi + bci\\
& = ac-bd + (ad + bc)i \end{align}\)
Taking our starting point as one again, this time we multiply by \(1 + i\) repeatedly.
\(\begin{align}1(1 + i) & = 1 + i\\
(1 + i)(1 + i) & = 2i\\
2i(1 + i) & = -2 + 2i\\
(-2 + 2i)(1 + i) & = -4\\
-4(1 + i) & = -4-4i\\
(-4 – 4i)(1 + i) & = -8i\\
(-8i)(1 + i) & = 8-8i\\
(8 – 8i)(1 + i) & = 16 \end{align}\)
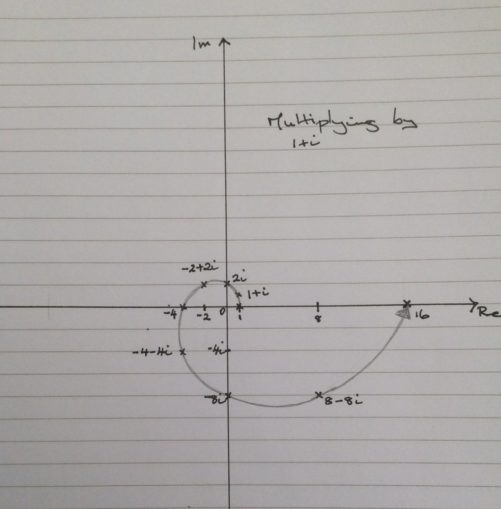
We still have a rotational locus but now in the form of a spiral.
Each multiplication by \(1 + i\) leads to a rotation by \(\pi/4\) and an increase in distance from the origin by \(\sqrt 2\).
This is because the point \(1 + i\) is at a distance \(\sqrt 2\) from the origin, \(0\), (by Pythagorus) and the angle that this point makes to the positive real axis is arctan \((1/1) = \pi/4\), where arctan is the inverse of the tangent function.
We look at an example.
Let :
\(z = 3 + 4i\) and \(w = 5 + 2i\)
Then :
\(zw = 7 + 26i\),
by the above formula.
We can break it down to see what is happening.
\((3 + 4i)5 = 15 + 20i\)
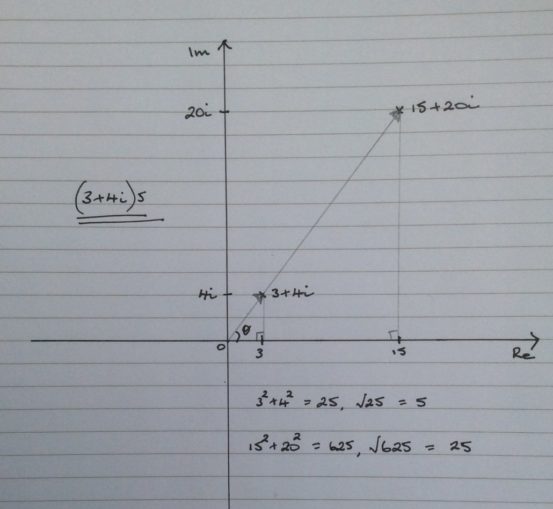
The point has been scaled up by a factor of \(5\) and the angle is left unchanged.
\((3 + 4i)2i = -8 + 6i\)
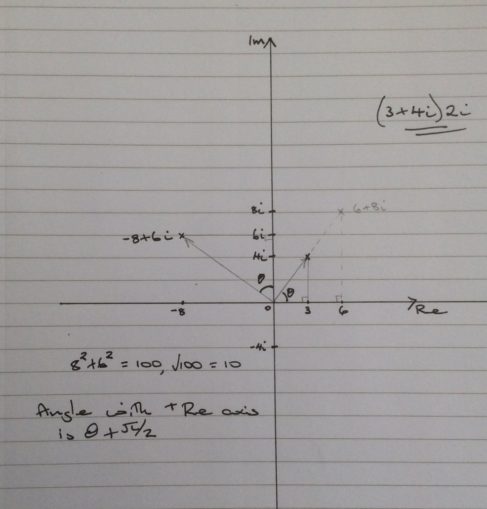
The point has been scaled up by a factor of \(2\) and rotated by an angle of \(\pi/2\).
The addition of these two parts gives us the point \(7 + 26i\)
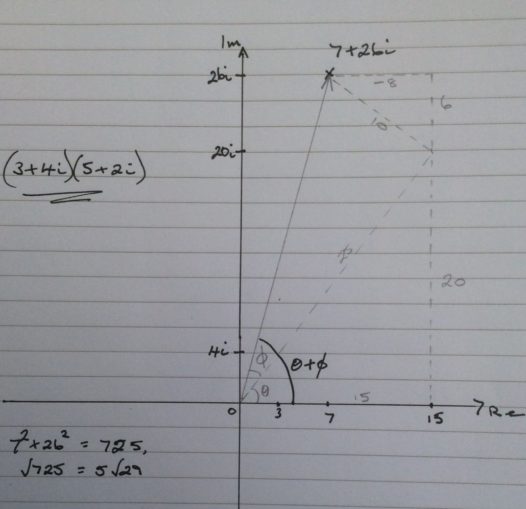
In terms of distances and angles (the polar representation) :
\(z = (r_1, \theta), w = (r_2, \phi)\) and \(zw = (r_1r_2, \theta + \phi)\).
\(z = 3 + 4i = (5, \theta)\), where \(\theta = \)arctan\((4/3) \approx 0.9273\) radians \(\approx 53.13^\circ\)
\(w = 5 + 2i = (\sqrt29, \phi)\), where \(\phi = \)arctan\((2/5) \approx 0.3805\) radians \(\approx 21.80^\circ\)
\(zw = 7 +26i = (5\sqrt29, \theta + \phi)\), where\(\theta + \phi =\)arctan\((26/7) \approx 1.3078\) radians \(\approx 74.93^\circ\)
Next time we will rotate in three different directions using the quaternions.
© OldTrout \(2019\)



