Introduction
I woke up one morning thinking, “I’ll write a few articles for GP about the gyroscope. How hard can that be?”. Hmm… Well it turns out that that was a really stupid idea. Are you listening brain? Well as Magnus Magnusson might have said, “I’ve damn well started the bloody project so I’m damn well going to finish it!”.
So here goes at explaining three different gyroscopic applications. I’m going to keep these articles as simple as possible. Maybe give you all some Christmas present ideas. There may be trouble ahead…
Number one – The Toy Gyroscope
Stocking fillers from Christmases past consisted of puzzle games, a Terry’s chocolate orange and perhaps a gyroscope. Eating a chocolate orange and playing with a gyroscope was “living the high life!” – well, for a geek like I. They are very simple in their construction (not the chocolate orange and most certainly not my good self):

The above photo is of a modern, cheap Chinese, gyroscope. The basic design hasn’t changed over the years. It’s simply a flywheel mounted in a circular steel frame. There’s a small hole in the bearing shaft that you wrap some string around. You pull that as hard as you can and the wheel spins up to – oh, I don’t know – at least ten thousand RPM. It then magically defies gravity. Simple.
Except it’s not.

Torque
This is where…err…things get complicated.
If I apply a force in the direction of arrow (A) the gyroscope moves in the direction of arrow (B). Unlike Newton’s third law of motion, which states that there will be an ‘equal and opposite reaction’, this thing goes off at an angle of ninety degrees. I suppose that’s an opposite reaction! The consequence of this interesting bit of physics has allowed the development (and stabilisation) of rocket technology.
To try and understand why this happens let’s first think about a door (on hinges, of course):

Consider the hinges as an “axis of rotation” (green arrow). Obviously, it requires more force to move the door at point (B) than it does at point (A). This force is measured as torque.
Another key (pun intended) consideration is the angle at which the force is applied. Closing (or opening) a door with your arm at ninety degrees to the axis of rotation is easy. Pushing up/down on the door does nothing – perhaps only to make it fall off of its hinges!
Angular Momentum (Yikes!)
Let me tie all of this gobbledegook together. Or at least try to make something coherent for you. Let’s start with this photo:
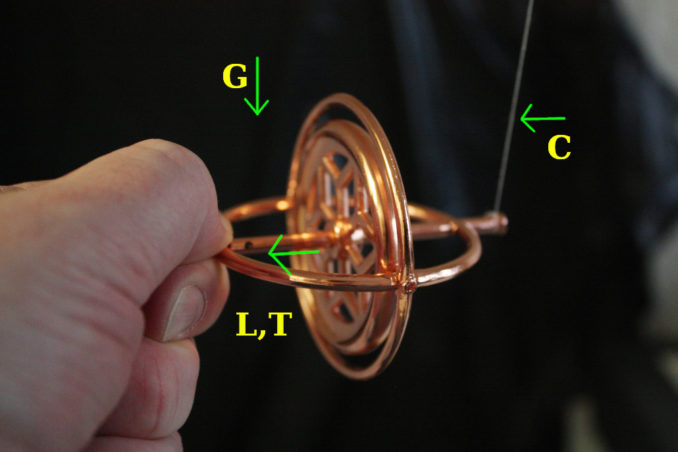
The cotton thread is like the hinges on a door. If I let go of the gyroscope it will simply fall to a vertical position. Gravity (G) makes it rotate around the cotton (C) support. We could say that the gyroscope precesses vertically.
We can consider the torque (T) and angular momentum (L) forces pointing in the same direction. So, gravity – like our arm pushing on a door – finds this very easy to do.
Now, let’s spin that thing up.

This is where it gets a bit more complicated, but nonetheless interesting. Let’s think of this as simply as is possible (because it does my head in!).
As the gyro flywheel rotates (the higher the speed, the better) the mass/atoms of said wheel are trying to fly outward away from the axis of rotation. There was an episode of ‘Myth Busters’ where they attached a compact disc to an angle grinder – very entertaining and very explosive!
Anyhow, the torque (T) created is now at ninety degrees to the angular momentum (L) – in other words, parallel to the fly wheel. This causes the gyroscope to precess (rotate) around point (P). Gravity (G) is – basically – trying to push a door off of its hinges!
Conclusion
Okay, I agree, that was a rubbish explanation. Without going into a lot of mathematics this subject is tricky to explain…to say the least. But I hope I’ve given you some idea(s) of what is happening.
In the next part I’ll have a go at planet earth. Well, I suppose, someone has to.
© text & images Doc Mike Finnley 2021



