Cmglee / CC BY-SA
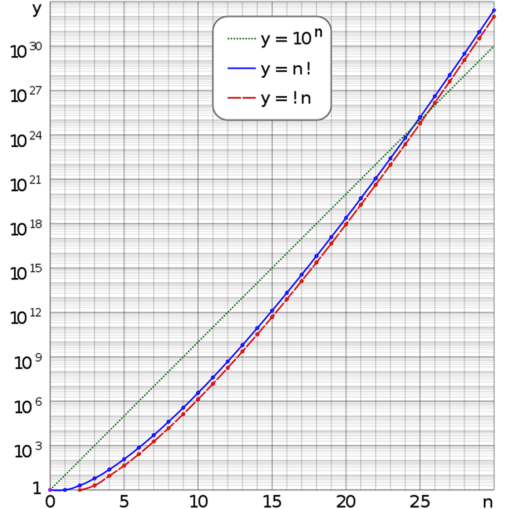
\displaystyle \lim_{n\to\infty} \frac {!n}{n!} = \frac {1}{e} \approx 0.3679…
Read as : the limit, as n approaches infinity, of subfactorial n divided by factorial n is equal to 1 divided by e which approximates to 0.3679, where e is Euler’s number, e = 2.71828…
The Hat Check Problem, as first described by Montmort in 1713, considers the following problem :
A group of n people enter a restaurant and check their hats. On leaving,
the hat-checker gives the hats back in a random order. What is the
probability that no one gets the correct hat?
In combinatorics, a derangement is a permutation in which none of the objects appear in their ordered place; that is, they have no fixed points.
The number of derangements of n is called the subfactorial of n and is denoted by !n. The number of permutations is n factorial denoted by n!.
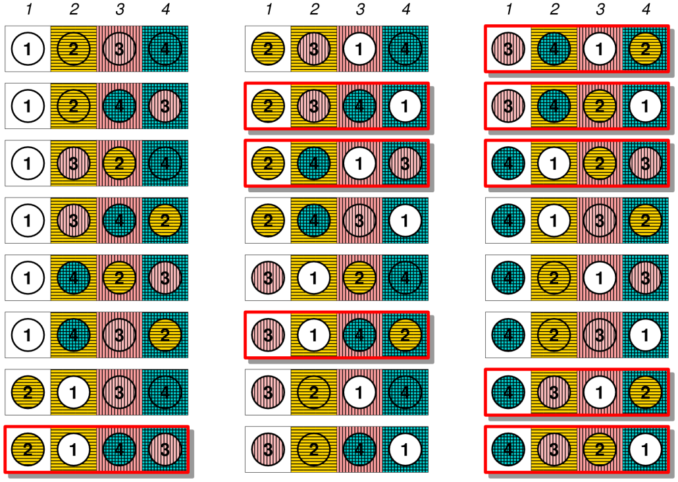
The permutations of the ordered set \{1, 2, 3\} are :
\begin{array}{c c c} \{1,2,3\}\\ \{1,3,2\}\\ \{2,1,3\}\\ \{2,3,1\}\\ \{3,1,2\}\\ \{3,2,1\} \end {array}
There are a total of 3! = 1\times2\times3 = 6 permutations. Of these, two are derangements, namely \{2,3,1\} and \{3,1,2\}. This because everything is out of place; there are no fixed points.
Thus, the probability of derangement is 2/6 = 1/3 = 33\%.
When n = 4, !n = 9 and n! = 24 and the probability is 9/24 = 3/8 = 37.5\%.
RokerHRO / CC BY
The numbers grow very quickly and the limit of 1/e is rapidly approached.
\begin{array}{c| c c c c} n & !n &n! &!n/n! & \%\\ \hline 1&0&1&0&0\\ 2&1&2&1/2&50\\ 3&2&6&1/3&33.33\\ 4&9&24&3/8&37.50\\ 5&44&120&11/30&36.67\\ 6&265&720&53/144&36.81\\ 7&1854&5040&103/280&36.79 \end{array}
By rearranging the above equation, we have the approximation :
\displaystyle !n \approx \frac {n!}{e}
By rounding to the nearest whole number, the value of !n is found.
When n = 4,
\displaystyle !4 \approx \frac{4!}{e} \approx \frac{24}{e} \approx 8.8291…
We can say :
\displaystyle !n = \left[\frac {n!}{e}\right],
where [ ] is the nearest whole integer function.
The following recurrence relationships also hold :
!n = D_n with D_1 = 0 and D_2 = 1
D_n = nD_{n-1} + (-1)^n
and
D_n = (n-1) (D_{n-1} + D_{n-2}),
where D_n is the nth derangement.
When n = 4,
D_4 = 4D_3 + (-1)^4 = 4\cdot 2 + 1 = 9
and
D_4 = 3(D_3 + D_2) = 3(2 + 1) = 9
© OldTrout 2020



