Cmglee / CC BY-SA
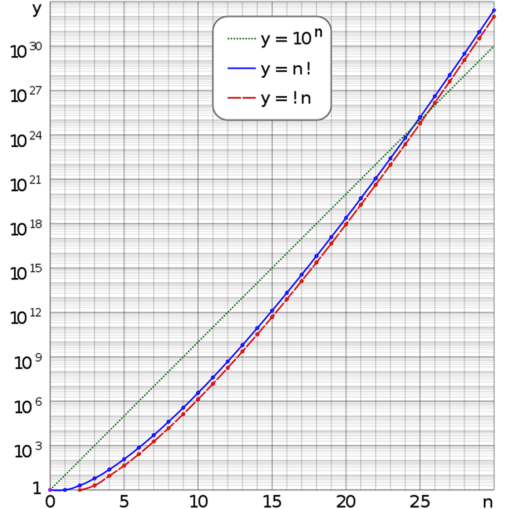
\(\displaystyle \lim_{n\to\infty} \frac {!n}{n!} = \frac {1}{e} \approx 0.3679…\)
Read as : the limit, as \(n\) approaches infinity, of subfactorial \(n\) divided by factorial \(n\) is equal to \(1\) divided by \(e\) which approximates to \(0.3679\), where \(e\) is Euler’s number, \(e = 2.71828…\)
The Hat Check Problem, as first described by Montmort in \(1713\), considers the following problem :
A group of \(n\) people enter a restaurant and check their hats. On leaving,
the hat-checker gives the hats back in a random order. What is the
probability that no one gets the correct hat?
In combinatorics, a derangement is a permutation in which none of the objects appear in their ordered place; that is, they have no fixed points.
The number of derangements of \(n\) is called the subfactorial of \(n\) and is denoted by \(!n\). The number of permutations is \(n\) factorial denoted by \(n!\).
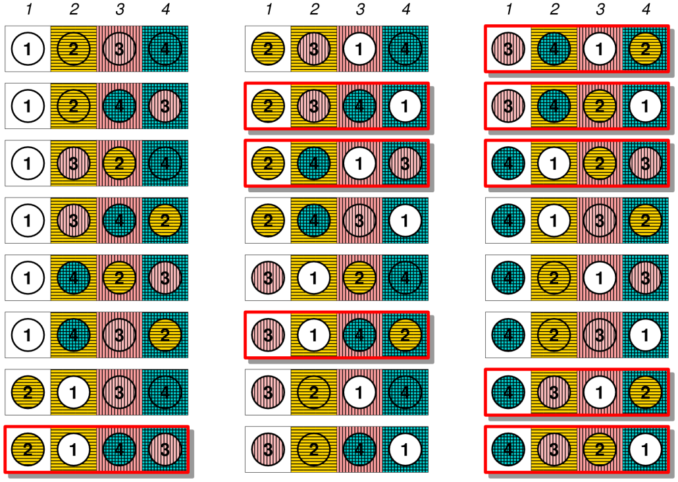
The permutations of the ordered set \(\{1, 2, 3\}\) are :
\(\begin{array}{c c c}
\{1,2,3\}\\
\{1,3,2\}\\
\{2,1,3\}\\
\{2,3,1\}\\
\{3,1,2\}\\
\{3,2,1\}
\end {array} \)
There are a total of \(3! = 1\times2\times3 = 6\) permutations. Of these, two are derangements, namely \(\{2,3,1\}\) and \(\{3,1,2\}\). This because everything is out of place; there are no fixed points.
Thus, the probability of derangement is \(2/6 = 1/3 = 33\%\).
When \(n = 4\), \(!n = 9\) and \(n! = 24\) and the probability is \(9/24 = 3/8 = 37.5\%\).
RokerHRO / CC BY
The numbers grow very quickly and the limit of \(1/e\) is rapidly approached.
\(
\begin{array}{c| c c c c}
n & !n &n! &!n/n! & \%\\
\hline
1&0&1&0&0\\
2&1&2&1/2&50\\
3&2&6&1/3&33.33\\
4&9&24&3/8&37.50\\
5&44&120&11/30&36.67\\
6&265&720&53/144&36.81\\
7&1854&5040&103/280&36.79
\end{array}
\)
By rearranging the above equation, we have the approximation :
\(\displaystyle !n \approx \frac {n!}{e}\)
By rounding to the nearest whole number, the value of \(!n\) is found.
When \(n = 4\),
\(\displaystyle !4 \approx \frac{4!}{e} \approx \frac{24}{e} \approx 8.8291…\)
We can say :
\(\displaystyle !n = \left[\frac {n!}{e}\right]\),
where [ ] is the nearest whole integer function.
The following recurrence relationships also hold :
\(!n = D_n\) with \(D_1 = 0\) and \(D_2 = 1\)
\(D_n = nD_{n-1} + (-1)^n\)
and
\(D_n = (n-1) (D_{n-1} + D_{n-2})\),
where \(D_n\) is the \(nth\) derangement.
When \(n = 4\),
\(D_4 = 4D_3 + (-1)^4 = 4\cdot 2 + 1 = 9\)
and
\(D_4 = 3(D_3 + D_2) = 3(2 + 1) = 9\)
© OldTrout \(2020\)



