Apparently, some subset of younger people are upset and intimidated about the use of full stops in text and other messages.
I am not sure what they would think about the ellipsis, … , or the exclamation mark, !, .
Mathematical notation is a language which is read with very precise meaning.
It makes use of letters from the Latin, Greek and Hebrew alphabets. These can be uppercase, lowercase, upright or italic. Boldface is used for matrices and vectors; when writing by hand these are underlined. Different calligraphies have specific meanings, for instance, Blackboard is used for sets. \mathbb{N} means the set of natural numbers.
Subscripts and superscripts play their part. Use is made of many symbols including some that are specific to areas of mathematics. For example, \forall and \exists are used in mathematical logic. The upside down A means ‘for all’ and the backwards E means ‘there exists’. \exists ! means ‘ there exists exactly one’.
Specific parts of the italic alphabet are used for different numbers :
a, b, c are constants or coefficients;
f, g, h are functions;
i, j, k are imaginary roots;
l, m, n are integers;
p, q are primes;
x, y, z are variables and
z,w are complex numbers.
We use different brackets in specific contexts :
( ) are parentheses or round brackets;
\{ \} are braces or curly brackets;
[ ] are square brackets;
\langle \rangle are angle brackets.
The ellipsis, … , means ‘to leave out. It can be read as dot-dot-dot. Would this subset of young people be frightened three times over?
We also use the exclamation mark as a symbol. That could frighten the horses!
n! is used to denote the factorial function. It is read as n factorial and also as n bang. It is the product of the natural numbers up to and including n. 0! is defined as 1. It is undefined for the negative integers.
5! = 1 \times 2 \times 3 \times 4 \times 5 = 120
We can use more than one bang. n!! is the double factorial function that gives the product of natural numbers of equal parity (odd or even). Thus,
5!! = 1 \times 3 \times 5 = 15 and
6!! = 2 \times 4 \times 6 = 48
The subfactorial function is denoted as !n. This calculates the number of derangements. I have written on this and will ask Swiss Bob to republish it.
It is commonly known as the Hat Check problem.
!5 = 44
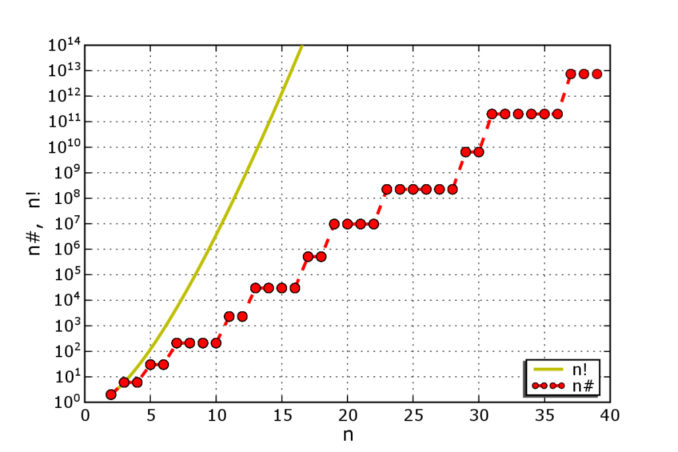
A favorite function of mine is the primorial function which is denoted by n \sharp. Read as n sharp. It gives the product of the primes up to n.
11 \sharp = 2 \times 3 \times 5 \times 7 \times 11 = 2310
12 \sharp = 2 \times 3 \times 5 \times 7 \times 11 = 2310
We will end with a tombstone which gives us a symbol that is used to denote ‘end of proof’ ■
© OldTrout 2020



