In the real numbers, \Bbb R, the following commutative laws hold :
x + y = y + x, for all x,y \in \Bbb R
xy = yx, for all x,y \in \Bbb R
Although these laws seem elemental, we wish to emphasise the fundamental nature of this property in the arithmetic of the real numbers.
The operation of addition is commutative.
3 + 5 = 5 + 3 = 8
The order in which we add does not alter the result.
The operation of subtraction is non commutative.
3-5 = -2\\ 5-3 = 2
When we change the order of the operands we obtain different solutions.
Multiplication is commutative.
2 \times 10 = 10 \times 2 = 20
Division is non commutative.
2 \div 10 = 1/5\\ 10 \div 2 = 5
We have other entities that have real numbers as elements where the commutative multiplication law does not hold.
Multiplication of square matrices (n \times n) is non commutative.
\mathbf A \mathbf B \neq \mathbf B \mathbf A
Note that upper-case, boldface, upright letters denote matrices.
Scalar multiplication of two vectors (the dot product) is commutative.
\mathbf a \cdot \mathbf b = \mathbf b \cdot \mathbf a
Vector multiplication of two vectors (the cross product) is non commutative.
\mathbf a \times \mathbf b \neq \mathbf b \times \mathbf a
Lower-case, boldface, upright letters denote vectors.
Commutativity holds for addition and multiplication when we extend the number system from the real numbers, \Bbb R, to the complex numbers, \Bbb C.
The complex numbers allow us to rotate in two dimensions.
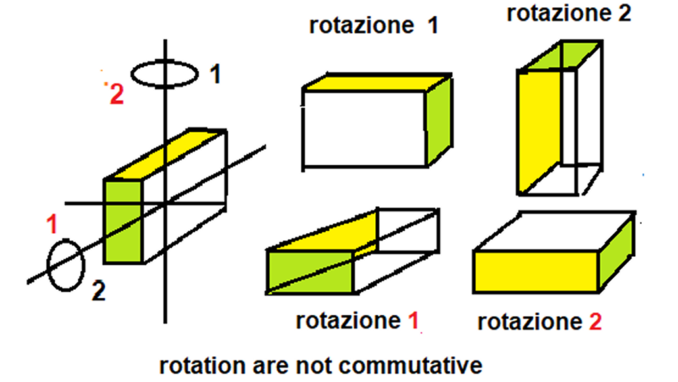
In order to rotate in three dimensions the number system is extended to the quaternion numbers, \Bbb H , where the commutative law of multiplication does not hold.
Order matters.
© OldTrout 2019



