The golden ratio is well known and is associated with the Fibonacci sequence of numbers. \(\varphi\) (phi) is the positive root of the quadratic equation \(x^2 = x + 1\).
The exact value is given by
\(\displaystyle \varphi = \frac{1 + \sqrt5}{2} \approx 1.61803\)
Its continued fraction is \([1; 1, 1, 1, …]\).
Less well known is the plastic ratio, denoted by \(\rho\) (rho). Here the word plastic is used in the sense of plasticity; capable of being shaped or moulded; malleable. The associated sequence of numbers is called the Padovan sequence.
It arose in architecture. Richard Padovan (an architect) attributed the sequence to Dom. Hans van Der Laan, ( a Dutch monk and architect) who named the ratio as the plastic number in 1928. The Church of St. Benedictusberg Abbey in the Netherlands was designed by van Der Laan using these plastic proportions. The plastic ratio can be thought of as a three-dimensional expression of the golden ratio.

The Padovan sequence of numbers begins :
\(1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, …\)
The Padovan sequence \(P(n)\) is defined by the initial values
\(P(0) = P(1) = P(2) = 1\)
and the recurrence relation
\(P(n) = P(n-2) + P(n-3)\)
For example,
\(P(12) = P(10) + P(9)\) which is \(16 = 9 + 7\).
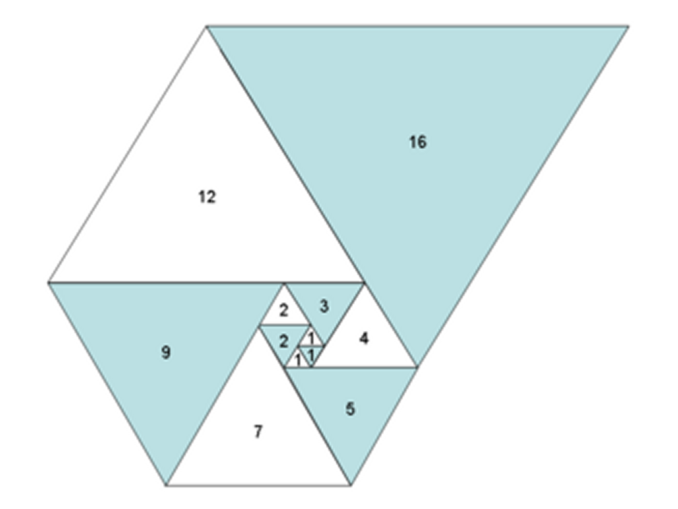
In the above image is a spiral of equilateral triangles with side lengths of the Padovan sequence. It is a visual proof that the sequence also satisfies the recurrence relation :
\(P(n) = P(n-1) + P(n-5)\)
For example,
\(P(12) = P(11) + P(7)\) which is \(16 = 12 + 4\)


Some values of the convergents are
\(\begin{array}{l|l}
Ratio & Decimal\\
\hline
1/1&1\\
1/1 &1\\
2/1 &2\\
2/2&1\\
3/2&1.5\\
4/3&1.\overline 3\\
5/4&1.25\\
7/5&1.4\\
9/7&1.\overline{285714}\\
12/9&1.\overline3\\
16/12&1.\overline3\\
21/16&1.3125\\
28/21&1.\overline3\\
37/28&1.32\overline{142857}\\
49/37&1.\overline{324}
\end{array}
\)
The limit of the convergents of consecutive Padovan numbers is
\(\displaystyle \lim \limits_{n \to \infty} \frac{P(n)}{P(n-1)} = \rho \)
Algebraically, this limit \(\rho\), is the unique real root of the cubic equation \(x^3 = x + 1\).
A cubic equation either has three real roots ( which may be repeated) or one real root and two complex roots.
\(\rho\) has the exact value
\(\displaystyle \rho = \frac{\sqrt[3]{9 + \sqrt69}}{18} + \frac{\sqrt[3]{9 -\sqrt69}}{18}\)
with an approximate value of
\(1.324 \, 717 \, 957 \,…\)
Its continued fraction is
\([1; 3, 12, 1, 1, 3, 2, 3, 2, 4, 2, 141, 80, …]\)
The powers of \(\rho\) rounded to 3 d.p.
\(\begin{array}{l|l}
\rho^n & Approx. Value\\
\hline
\rho^{-5} & 0.245\\
\rho^{-4} & 0.325\\
\rho^{-3} & 0.430\\
\rho^{-2} & 0.570\\
\rho^{-1} & 0.755\\
\rho^0 & 1\\
\rho^1 & 1.325\\
\rho^2 & 1.755\\
\rho^3 & 2.325\\
\rho^4 & 3.080\\
\rho^5 & 4.080
\end{array}\)
Using the two recurrence relations we can divide a square into three rectangles each with the same aspect ratio of \(1 : \rho^2\).
Start with a square of side length \(\rho^3\).
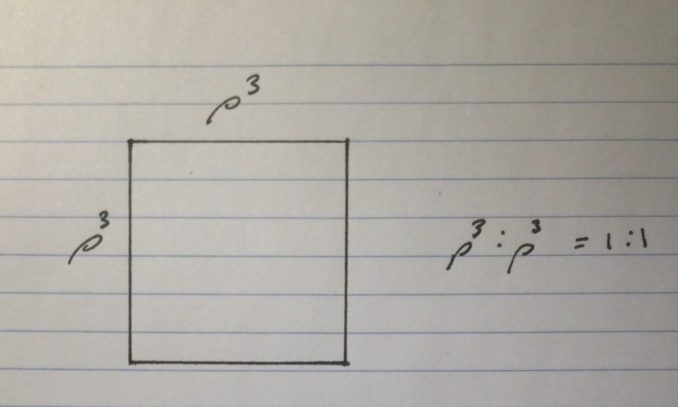
We can divide this square with a line into two rectangles since \(P(n) = P(n – 2) + P(n – 3) \equiv \rho^3 = \rho + 1\).
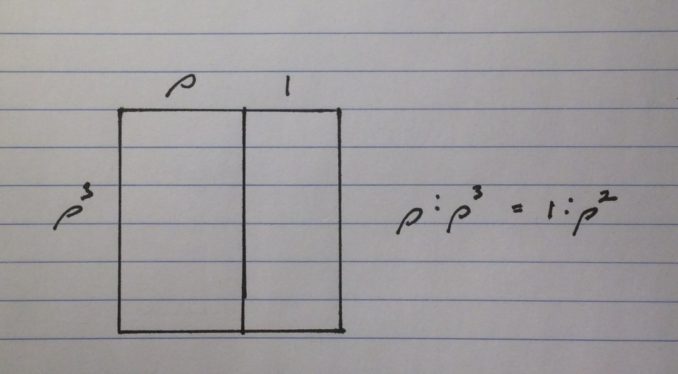
The larger rectangle has aspect ratio \(\rho : \rho^3\) which is equivalent to \(1 : \rho^2\)
We can divide the small rectangle with a line since \(P(n) = P(n – 1) + P(n – 5) \equiv \rho^3 = \rho^2 + \frac{1}{\rho^2}\).

Now the medium rectangle has aspect ratio \(1 : \rho^2\) and the small rectangle has aspect ratio \(\frac {1}{\rho^2} : 1\) which is equivalent to \(1 : \rho^2\).
You can check that the numbers add up by using the table of the powers of \(\rho\).
© OldTrout \(2020\)



