In part one we covered the basics of motion, some definitions, a few useful equations, units of measurement and similar governing constant linear acceleration.
This time we are going to look at Newton’s three laws in bit more detail and cover what they actually mean in turn and how you can prove them for yourself, this will provide the building blocks to start looking at a range of examples and a few useful techniques to evaluate these before we go further still.
Recap, Three laws of motion
First Law
In an inertial frame of reference, an object either remains at rest or continues to move at a constant velocity. Unless acted upon by a force.
Second Law
In an inertial frame of reference, the vector sum of the forces \(\mathbf{F}\) on an object is equal to the mass \(m\) of that object multiplied by the acceleration \(\mathbf{a}\) of the object: \(\mathbf{F}=m\mathbf{a}\) (it is assumed here the mass is constant)
Third Law
When a body exerts a force on a second body, the second body simultaneously exerts a force equal in magnitude and opposite in direction on the first body.
We firstly need to establish our frame of reference, we will, in true physics style, start out with an infinitely large void containing nothing other than what we will later put into it. There is no atmosphere here, a bit like when a group of scientists hold a party. We will not go into where this infinitely large void is, or what we did with the packaging it arrived in.
Because there is nothing in here, there is no gravity, it’s a perfectly neutral space.
We can establish a coordinate system in three dimensions here with axis x, y & z, however we will only be moving in the x & y planes as its much easier to draw and less confusing, given its still not Monday. This provides our frame of reference, everything is measured relative to our coordinate system.
For those wishing to experiment at home, and are finding is a bit hard to locate somewhere to put an infinitely large void a useful analogy is a flat and level glass table top, this is sooth enough (clean the fried egg and biscuit crumbs up first) that with say a glass marble we can ignore friction and we will only be moving slowly so can ignore air resistance.
If you are serious bored or just a suspicious cynic if you have suitable equipment to measure time, distance and velocity you can confirm the five basic equations from last time.
First Law
We stick an object at the origin, coordinates (0,0,0), we will assign this object a mass of 1kg, we will also assign in an initial velocity of zero so its not moving.
In effect, stick a glass marble in the middle of the table.
Now watch.
Dull isn’t it, the object doesn’t move, the marble remains exactly where it is.
In the case of our object its because no external force it acting upon it, in the case of the marble that’s not quite true, gravity is acting but the table provides a reaction to resist this, so again the marble doesn’t move.
We can thus observe the first part of the first law, the object is at rest and does indeed remain there. The beauty of hypothetical objects and glass marbles is that they don’t get bored.
Leopards however do, so what we want to do is to apply a force and observe what happens. Now we can do this mathematically to our object, the previous formula indicate mathematically what will happen, but from an experimental perspective poke the marble with a paw and watch.
You have applied a force to the marble, by poking it, and the marble has as a result started to move in the direction you poked it. Maths aside you have provided a force to act upon the object, the first law indicates something will happen an indeed it has.
Continue to watch, the marble, now moving, will keep moving until it falls off the edge of the table. Our hypothetical object will keep moving as well. In practice the marble is slowing down very slowly due to friction but in the space of a typical table you won’t notice that. If you measure the veolocity, say by filming the marble on your phones video camera, then replay the video frame by frame you will observe the velocity is effectively constant.
This demonstrates the first law, the first law basically says objects are lazy, they tend to do nothing unless forced to. The key principle is that unless some sort of force is provided the situation remains stable and constant.
Until the marble falls off the table, note this also can be used to demonstrate the first law, now the marble has gravity acting upon it and can be seen to react by falling and accelerating. If again you film this and play back frame by frame you will see (and can measure) the acceleration due to gravity. The marble won’t be falling fast enough for air resistance to play a part unless you have a seriously high table.
Our hypothetical object lacks gravity so doesn’t “fall off”
We can visualise this thus:
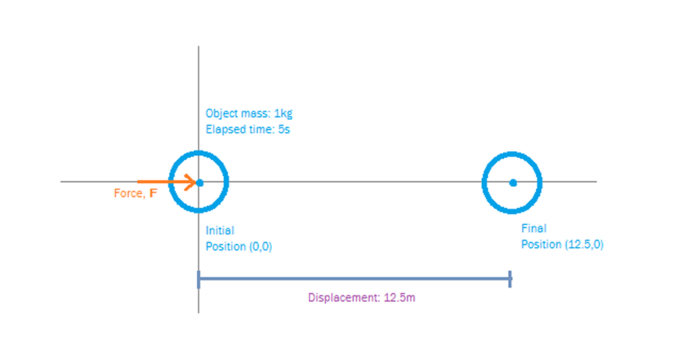
Our object, shown in blue, starts at the origin of our frame of reference, with an initial velocity of zero. We apply a force of 1N as shown.
The equation: \(\mathbf{F}=m\mathbf{a}\) tells us that the result of this is an acceleration of 1ms-1. Note this applies while the force is in effect, here we apply this constant force for 5 seconds. Note that we only need the objects mass and the force to determine the acceleration, we can then use the equations from the previous part to determine what happens to our object. we want to know the displacement and its final velocity.
We use the first equation to determine the final velocity: \(\mathbf{v}=\mathbf{u}+\mathbf{a}t\), since the initial velocity is zero this tells us our final velocity will be \(5ms^{-1}\).
We can use the second equation to determine the displacement: \(\mathbf{s}=\mathbf{u}t + \frac{1}{2}\mathbf{a}t^2\), again since the initial velocity is zero the first part resolves to zero, the second part tells us we have moved \(12.5m\).
We are also able to slice the time up into 1 second increments, this will allow us to see the motion of the object at stages, this will demonstrate the acceleration, because I’m lazy I asked a spreadsheet to do this for me, this incremental method of visualisation is very useful to understand what is actually going on, it also allows changing the acceleration as we will see later.
| time (\(t\)) | acceleration (\(\mathbf{a}\)) | velocity (\(\mathbf{v}\)) | displacement (\(\mathbf{s}\)) |
|---|---|---|---|
| \(s\) | \(ms^{-2}\) | \(ms^{-1}\) | \(m\) |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0.5 |
| 2 | 1 | 2 | 2 |
| 3 | 1 | 3 | 4.5 |
| 4 | 1 | 4 | 8 |
| 5 | 1 | 5 | 12.5 |
This can be visualised thus:
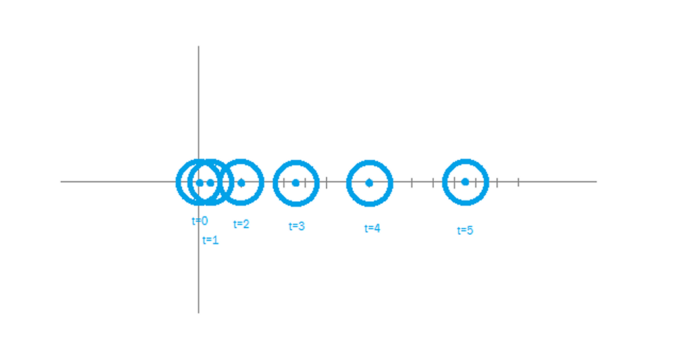
As can be seen from the table and the diagram each second the object is moving faster and thus in each second it covers more distance than the last.
This process can be seen (though in the vertical direction) when we consider acceleration due to gravity, however its not easy to accurately measure the time for an object to fall under gravity, if you have the equipment though it does work.
But what if you don’t?
This is where we can use the vector nature of forces to our benefit, and incidentally also prove how we can resolve vectors and also the third law in the process, in part three we will do just this, and provide a real world experiment you can do yourself to determine the acceleration due to gravity in the comfort of your own home.
No liability is accepted for harm done to use when the domestic authorities find out just what you have done to the kitchen table however.
In the next part we will start looking at acceleration due to gravity.
© Leopard 2020
The Goodnight Vienna Audio file



