
© Andrew Dunn, 5 November 2004. CC BY-SA 2.0
In part four we covered the basic principles of constant rotational acceleration, moment of inertia and related topics, in this part we will take this and demonstrate what this means.
When we looked at constant linear acceleration we saw that Forces can be combined into a net force to see the net effect, this is managed by simple vector addition. With rotational mechanics there is a similar principle, this is the principle of moments. A moment being a force applied at a distance, which you will recall is the definition of Torque.
Newton’s three laws also apply to rotation and can be written thus:
First Law
In an inertial frame of reference, an object either remains at rest or continues to move at a constant Angular velocity. Unless acted upon by a Torque.
Second Law
In an inertial frame of reference, the sum of the Torques T on an object is equal to the moment of inertia I of that object multiplied by the angular acceleration α of the object: T = Iα
Third Law
When a body exerts a Torque on a second body, the second body simultaneously exerts a Torque equal in magnitude and opposite in direction on the first body.
* * *
In effect as before things continue to do what they are doing, unless some external influence is present. Just as in the linear world linear momentum is preserved (things keep moving) in the angular world angular moment is also preserved, however as we have seen an object can change its moment of inertia by changing its mass distribution.
Consider a simple example, a figure skater spinning on the spot with their arms outstretched, roughly thus:
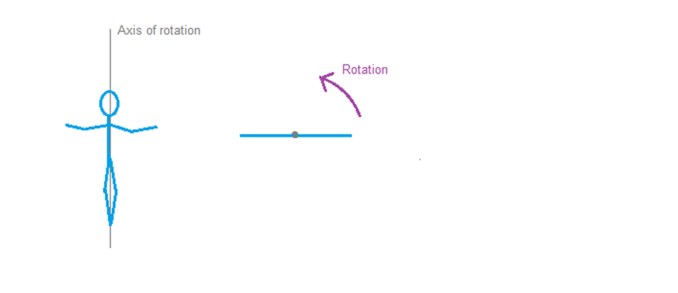
This is essentially the same as the bar diagram in part 4, the skater will have an angular velocity ω0 and a moment of inertia I0. The product of these two values is conserved.
So what does that mean? Well if we ignore external forces such as friction we can multiply the angular velocity by the moment of inertia and get a result. This result won’t change, so if either the angular velocity or the moment of inertia change, the other changes to maintain the product.
We have seen that if the mass distribution changes, e.g. by the skater lowering their arms the moment of inertia will vary, lowering their arms will decrease the moment of inertia by bringing the mass closer to the centre. To conserve angular momentum this means the skaters angular velocity will increase.
The converse is also true, extending their arms will slow them down.
This is a perfect excuse to watch figure skating and call it “research”
“and that, m’lud, is how I came to acquire of all these videos…”
Ahem..
Safer topics…
Back to our bar from the last part:

We know the moment of inertia for this bar is 0.25 kg m2. Lets see what happens if we try to move it.

We apply a force of 1N, we know this is 1m from the pivot thus we know we are applying 1Nm of torque.
We know that T=Iα, we can thus determine that our angular acceleration will be equal to T/I = 1/0.25 = 4 rad s-2.
According to ω = ω0 + αt we thus know after 1 second our angular velocity will be 4 rad -1. We also know that according to θ = θ0 + ω0t + ½ αt2 our final angular displacement will be 2 (radians).
Note here by using radians as the angle of measurement we have completely avoided using π at any point.
Right, so how do you verify this experimentally?
Well, what we do is to a large extent work backwards and validate the moment of inertia of a system, then vary a force and predict the change, then validate that change.
the set up looks something like this, the difficult bit being arranging for the constant force and thus constant torque.

What we have is an object (blue) held in a frame (brown) able to spin freely upon its axis (grey), this is our test object to which we will apply a constant force, creating a constant torque around its centre of rotation.
We do this by coiling string (amazing stuff string) around the object without letting the string overlap itself, this is run over a roller, which is considered to be frictionless but in practice as long as its low friction like the objects bearings its good enough to show the principle. We then hang a known mass on the end of this.
Gravity acts on the mass, accelerating is downwards at 9.81ms-2 this generates a reaction in the string, which in turn acts as a force on the object, its moment of inertia acts to resist this, exerting a force on the string, which exerts a force on the mass, slowing it down.
The key is the force from the mass on the object via the string is constant.
Ok, lets plug in some real world values and see what comes out.
We will use a 1kg mass, thus this will, via F=ma, exert a force of 9.81N on the object through the string. If we assume the string is wrapped on a 2cm diameter cylinder as part of the object this will exert a torque of 9.81N x 0.02m = 0.1962 Nm on our object.
Our object starts with an angular velocity of zero. We assume the mass can fall 1m, so the length of string we pull will be 1m, since we know the circumference of the cylinder is 2πr, and we know r we can determine that the circumference of the cylinder is 0.04π m, thus each rotation of this cylinder (2π radians) will use 0.04π of string, the length of string we have is 1m, thus we will generate 1/0.04π rotations, this resolves to: (1/0.04π) * 2π, which allows the values for π to cancel out and results in an angular rotation of 50 radians.
So we now know the starting angular displacement, the final angular displacement and the torque applied. What we do not know is the moment of inertia of the object or the time taken for the mass to fall – experimentally we can observe the time taken to fall, we assume this takes 10 seconds here, actual measurements will depend upon the system itself.
Using ω = ω0 + αt we can thus re-arrange and determine the angular acceleration, 50/10 = 5 rad s-2. Then using T=Iα and using the value of T we found earlier we can determine the moment of inertia for this system to be 0.1962/5 = 0.03924 kg m2.
You can then take this value and change the system in a known way, predict the impact and then experimentally confirm it.
The easiest thing to change is the mass of the falling weight, double it to 2kg, you would expect the result to be the mass falling faster, but how much faster?
The force on our object, and thus the torque, have doubled, you would thus expect for the same moment of inertia the angular acceleration to double, to 10 rad s-2. We can then use ω = ω0 + αt and re-arrange for time to see that we have a time of 50/10 = 5 seconds.
Doubling the mass has halved the time, actually confirming that experimentally is left to the reader, but this is in line with what you would expect from a theoretical system.
Note in practice the time will be slightly more than half due to friction in the system being in proportion to the speed and the speed will be greater here, but set it up right and it will be pretty close.
You will also then observe the object continues to rotate until it eventually gets tangled in the string, at which point I suggest running away and pretending the mess in the kitchen is something for which you are not to blame.
* * *
Ok, so up to this point we have covered constant linear acceleration and motion, we have also covered constant angular acceleration and the interesting and important concept of moment of inertia.
We have only touched upon the whole concept of “moments”, which is a significant rabbit hole all by itself.
In the next part we will take a quick detour to consider how gravity works, and how to determine the effect of it upon objects.
© Leopard 2020
The Goodnight Vienna Audio file
Audio Player



